Julia Chatain

I am a Senior Scientist at the Singapore-ETH Centre, building the Future Embodied Learning Technologies (FELT) programme, and I am interested in math education, HCI, XR, AI, and embodiment.

Grounding Mathematics

Mar 2023

Mathematics is a useful skill to learn, even for students who do not wish to become mathematicians. One of the goals of mathematics is to gain understanding of the patterns of the world, in order to model and predict future outcomes. Recent years shed light on the importance of mathematics, for example to understand and take action during the COVID-19 pandemic or the general climate crisis. However, most students find mathematics useless and disconnected from the real world, and several countries are witnessing a worrisome decline in mathematics ability. This means, we argue, that we should challenge our assumptions about how to teach mathematics, specifically as the way we teach mathematics currently does not enable students to understand it well enough to transfer their skills to other classes, nor outside of the classroom setting.

Researchers and educators tackling this issue have argued that, although mathematics is often considered as a Platonic ideal that cannot directly be sensed or manipulated, mathematics rather is a social and malleable process that arises from our sensorimotor experiences of the world. For example, arithmetic can be seen as manipulation of object collections. Similarly, the concept of infinity can be related to our way of expressing something too large for our senses to perceive, while continuity may arise from sequences of elements too small for us to sense. Simply put, mathematics is embodied, and, although not all experts agree on the implications of this theory, there is undeniable evidence that our bodies play an important role in learning mathematics. As a consequence, when designing learning activities, we need to facilitate gesture production, and support sense-making of bodily actions.

Meanwhile, Virtual Reality (VR), a technology heavily focused on bodily movement and manipulations, became more affordable and widespread. Using a wireless Head-Mounted Displays, VR can immerse learners' sensory channels into another world, digitally manufactured. Using hand-tracking technologies, VR seems particularly suitable to support embodied learning activities. With VR, we could create the MathLand imagined by Papert, a world of mathematics where learners can explore and manipulate mathematical objects. But is VR truly the solution to support the transition towards embodied learning of mathematics?

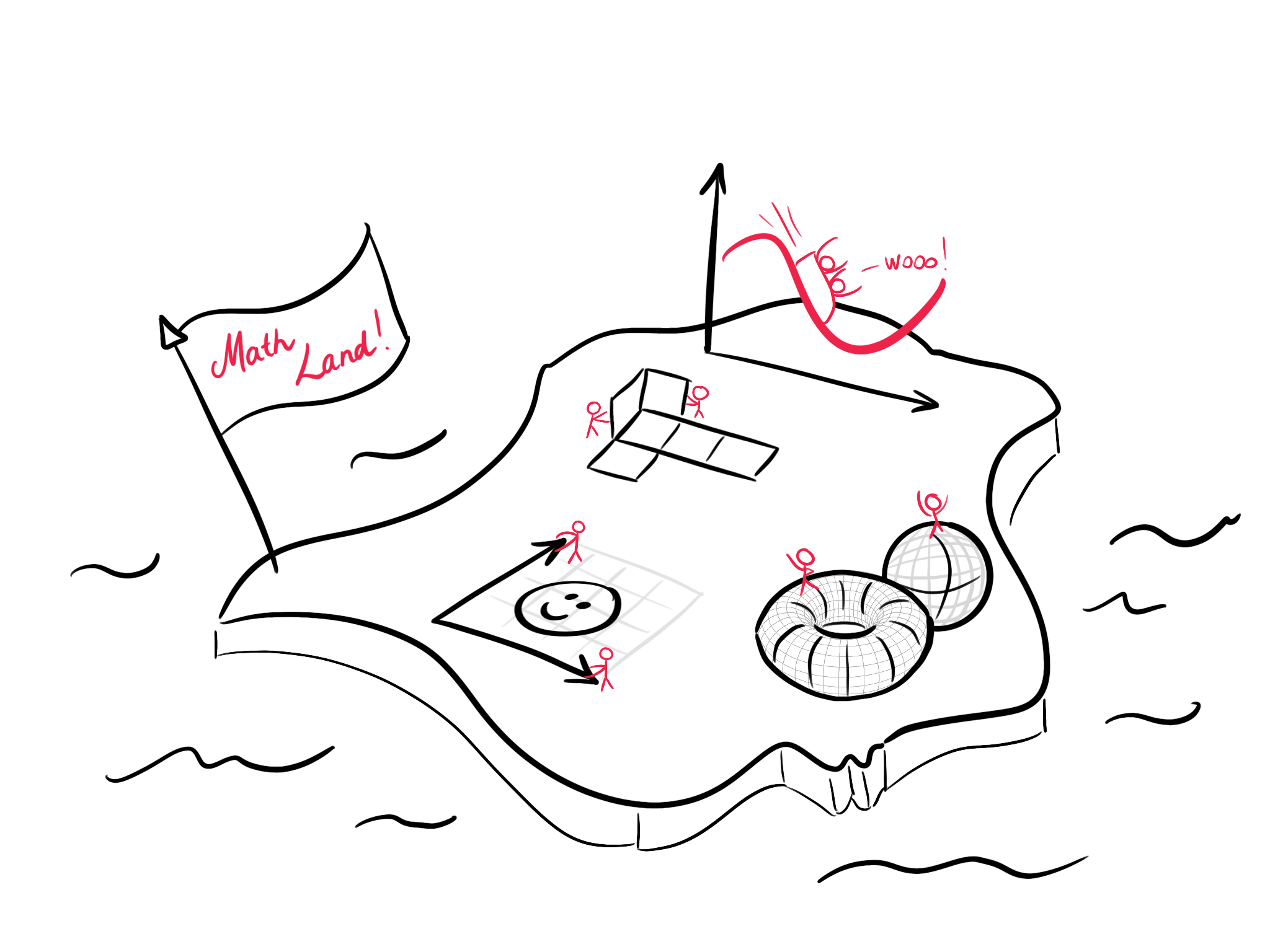
an island with different mathematical objects that students can play with, such as topological objects, curves as roller coasters, linear algebra with manipulable vectors, or developed cube to assemble

Although the idea of using VR to implement embodied learning activities seems promising, VR interaction research does not leverage actual theories of embodied learning. Specifically, we identified three main challenges in this field. First, there is a lack of empirical studies evaluating the effect of VR embodied learning activities. Second, only a handful of studies address higher education specifically. Third, there are no design guidelines for embodied learning activities in VR focusing specifically on interaction. Considering these challenges, our work addresses the following research question:

How to design embodied interaction to support embodied sense-making of mathematics?

a person is manipulating a function's graph in VR. In the background is a mountain and a water pipe system.

We ground our work in three meanings of embodiment: Embodied cognition relates to the role of learners' bodies in cognition, embodied interaction relates to the role of users' bodies in interaction, and avatar embodiment relates to the perception of a digital body as one's own. Within this framework, we address these challenges through six contributions, summarized below.

Designing the digital avatar

(project) (publication)

Looking at embodied interaction at the level of the avatar, we propose “Digital Gloves”, a novel input mechanism that supports embodied interaction and reduces split-attention effect by co-locating input and display on the users' hands. Through two user studies, we demonstrate the potential of our mechanism for more intuitive, enjoyable, and effective gaming and learning experiences. We offer recommendations to best design activities using our mechanism as well as suggestions for future applications.

A pinball game, a racing game, and a comparison activity

Designing the interaction

(project) (publication)

Focusing on the interaction level, we offer an empirical evaluation of the impact of the degree and type of embodiment on usability and learning outcomes. To do so, we designed an embodied activity to learn about derivatives. Our results reveal that although the degree of embodiment only impacts the duration of the activity, the type of embodiment impacts manipulations and learning outcomes. We offer an explanation of these results in terms of mathematical meanings highlighted by different types of embodiment, and conclude with design recommendations for VR embodied learning activities.

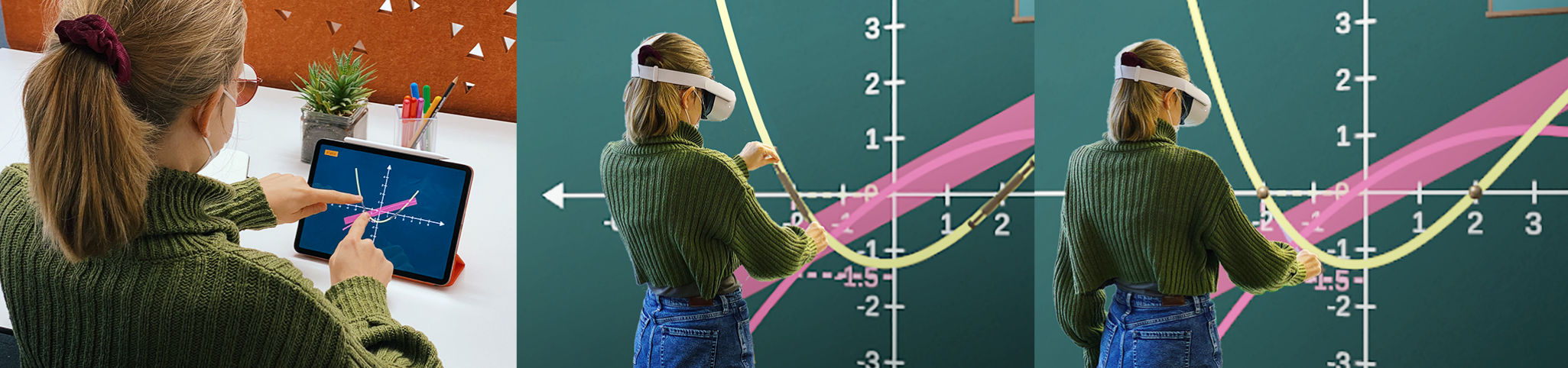
Three different ways of learning derivatives using embodied interaction: direct-embodied interaction on tablet, direct-embodied interaction in Virtual Reality, and enacted interaction in Virtual Reality

Designing the context of the interaction

(project) (publication)

Looking at the context of the interaction, we then conceptualize embodiment as a form of concreteness, and demonstrate the grounding affordances of embodied concreteness. To do so, we designed an embodied activity in VR to teach graph theory to bachelor students. Our activity builds on embodied metaphors by representing graphs as water flow systems. Our results show that students using our activities feel that the activity highlights the relevance of the topic best, and also feel better prepared for the subsequent lecture. Moreover, unlike an activity focusing on manipulation only, our activity does not impair transfer abilities.

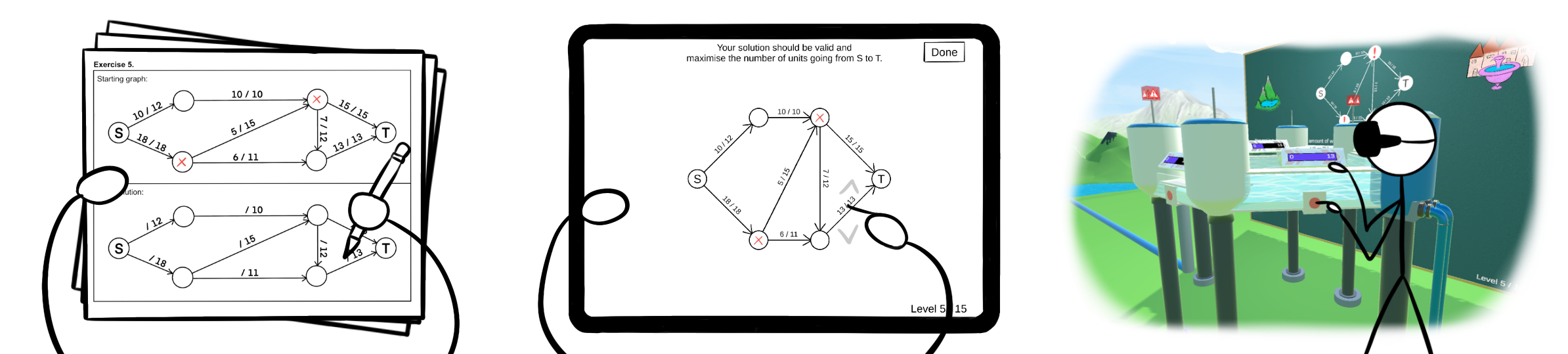
The figures contains three pictures, in doodle style. On the first figure, a character solves a graph theory problem on paper with an abstract representation. On the second figure, on tablet with an abstract representation. On the third figure, in Virtual Reality with a relatable and embodied representation. The graph is always the same and the character always interacts with the same edge.

Designing for individual differences in learners

(links coming soon)

As learners are at the core of the learning experience, we also explore the design space of embodied interaction for sense-making focusing on the individual differences among learners. Specifically, we explore two contexts. First, we look into an intuition-building activity where learners are directed towards specific bodily actions. Second, we look into an intuition-probing activity where learners spontaneously perform bodily actions. Specifically, we look at the role of individual differences and we aggregate the results from both studies to offer general design recommendations as well as directions for future research on sense-making embodied interaction in VR.

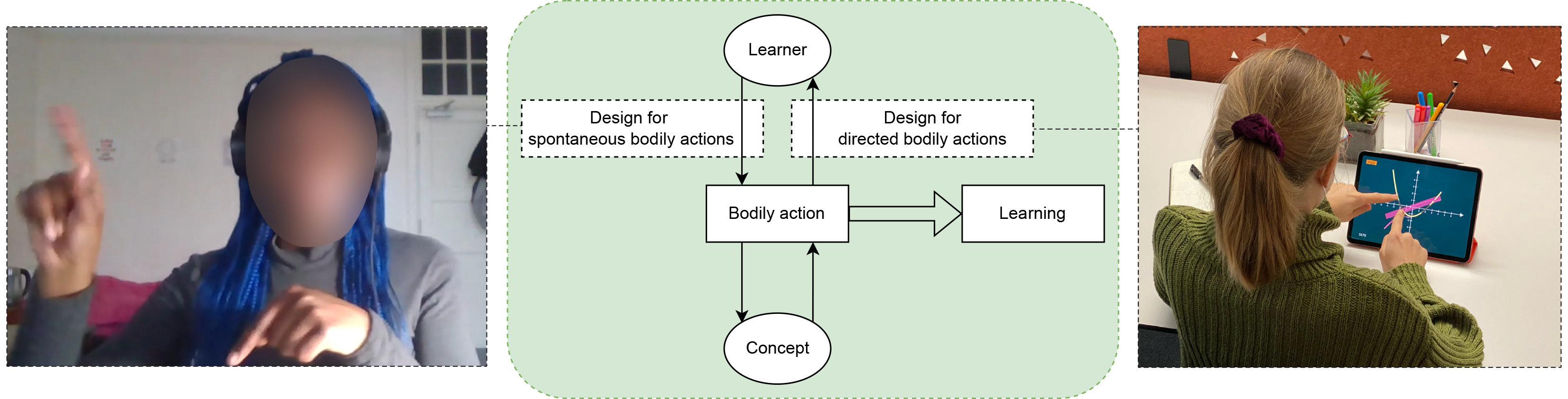
The left picture shows an anonymized participant representing a slope in the air using both pointing fingers. On their side is a picture of a function's graph that they are describing. The right picture shows a woman manipulating a function's graph on a tablet using both pointing fingers on a specific point of the function to adjust its slope. In the middle, there is a system representation with several elements. Learner in a circle with bidirectional arrows towards a bodily actions box. This box has bidirectional arrows towards a Concept circle. The box also has a double arrow towards a learning box. The arrow from the learner to the bodily action contains the label Design for spontaneous bodily actions, and the arrow on the other direction contains the label Design for directed bodily actions.

Supporting transition to formalisms

(publication)

As our activities so far focus on intuition building, we then explore how to reconnect the embodied activities with formal representations of mathematical objects. In this project, we designed and evaluated two prototypes for input of mathematical expressions in Virtual Reality.

A character types in mathematical formulas in VR, either by tapping on a keyboard or by dragging and dropping elements to the formula.

Defining the embodiment landscape

(project) (publication)

Finally, based on this experience, we offer an interdisciplinary framework for embodied learning and describe its relevance through several use cases. From this we draw several design considerations for VR embodied learning interactions: (1) consider the meaning highlighted by the interaction and its context and how it relates to the meaning being learned, (2) consider desirable difficulties in interaction to support deeper sense-making of bodily actions, and (3) consider breaking avatar-body morphological similarity to design semantic avatars, that is, avatars designed to apprehend a specific concept and highlight a specific meaning.

Three pictures. 1. A person has an arm folded and an arm extended. These two arms represent the x and y axis in a horizontal plane. The plane is distorted, as one arm is longer than the other. On the plane are 3D houses and trees to show the distortion. 2. A woman interacts with a function curve in VR. The display also shows the derivative, which the woman manipulates through a digital rotating angle. 3. A man interacts with a pipe system representation of a graph in VR. He presses a button on a pipe with one hand, and adjusts the level of the water in the pipe with the other hand.

Defense video

Team

Publications

🏆 Chatain, Julia. "Embodied Interaction in Virtual Reality for Grounding Mathematics". Doctoral dissertation. Recipient of the ETH medal for outstanding dissertation. (link) (pdf)

Chatain, Julia, Manu Kapur, Robert W. Sumner. "Three Perspectives on Embodied Learning in Virtual Reality: Opportunities for Interaction Design". In CHI EA ’23: Extended Abstracts of the 2023 CHI Conference on Human Factors in Computing Systems. (2023) (link) (pdf)

Chatain, Julia, Robert W. Sumner, Manu Kapur. "Embodied interaction in virtual reality for learning mathematics." In the 20th Biennial EARLI Conference. (2023).

Chatain, Julia, Rudolf Varga, Violaine Fayolle, Manu Kapur, Robert W. Sumner. "Grounding Graph Theory in Embodied Concreteness with Virtual Reality". In TEI '23: Proceedings of the Seventeenth International Conference on Tangible, Embedded, and Embodied Interaction. (2023). (link) (pdf)

Chatain, Julia, Virginia Ramp, Venera Gashaj, Violaine Fayolle, Manu Kapur, Robert W. Sumner, Stéphane Magnenat. "Grasping Derivatives: Teaching Mathematics through Embodied Interactions using Tablets and Virtual Reality". In Interaction Design and Children (IDC’22). (2022). (link) (pdf)

Sansonetti, L., Chatain, J., Caldeira, P., Fayolle, V., Kapur, M., & Sumner, R. W. (2021). Mathematics Input for Educational Applications in Virtual Reality. In ICAT-EGVE 2021-International Conference on Artificial Reality and Telexistence and Eurographics Symposium on Virtual Environments. Eurographics Association. (link) (pdf)

Chatain, Julia, Danielle M. Sisserman, Lea Reichardt, Violaine Fayolle, Manu Kapur, Robert W. Sumner, Fabio Zünd, Amit H. Bermano. 2020. DigiGlo: Exploring the Palm as an Input and Display Mechanism through Digital Gloves. In Proceedings of the Annual Symposium on Computer-Human Interaction in Play (CHI PLAY ’20), November 2–4, 2020, Virtual Event, Canada. ACM, New York, NY, USA, 12 pages. (link) (pdf)

Project page on the Future Learning Initiative website. (link)

Math Land is inspired by: Papert, S. A. (1990). Mindstorms: Children, computers, and powerful ideas. Basic books.

Defining the embodiment landscape. (link)

Designing the digital avatar: Digital Gloves. (link)

Designing the interaction: Grasping derivatives. (link)

Designing the context of the interaction: Grounding graph theory in embodied concreteness. (link)

More coming soon...