Concrete Taxonomy

Concreteness and abstraction are key in educational research in mathematics, both when discussing the nature of mathematics in itself, but also when exploring how to learn and teach mathematics. However, while the terms concrete and abstract are often used in the field, they are not always used with the same meaning. For example, the word concrete can be used to mean specific, relatable, visual, tangible, while the word abstract can be used as general, rigorous, vague, symbolic. While several scholars have emphasized the need for a multidimensional and fine-grained framework to articulate these differences in meaning, we further argue that it is crucial to precisely define how the terms concrete and abstract are actually used by the research community. Towards this goal, we offer three contributions. First, we empirically and systematically identify the various meanings of concrete and abstract used in the literature. Second, we offer a data-informed taxonomy to organize this semantic landscape and support research inquiry. And third, we offer templates for the design of future mathematics education interventions and studies.

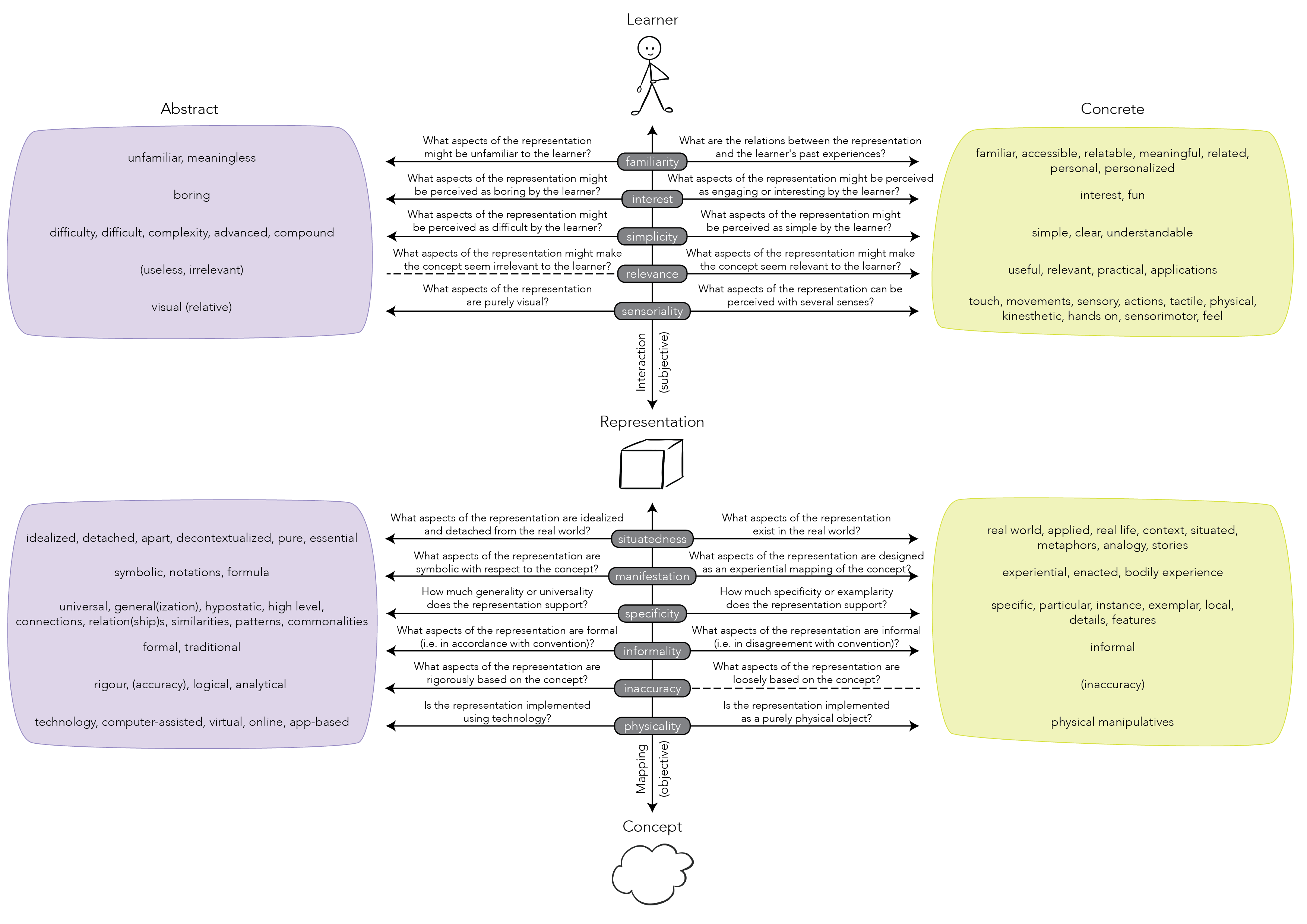
Final taxonomy

Materials

We hope that this taxonomy supports future work, in three ways, and we provide templates to support these endeavors.

First, with our taxonomy, we focused on providing a complete overview of the meanings of the terms "concrete" and "abstract" in the mathematics education literature. Now, the relationships between these axes should be further investigated: What relationships have been explored, and validated or disproved? What gaps remain to be explored? We offer an initial discussion in this paper, but we believe that pursuing this approach thoroughly and with the wider community can raise critical questions and inquiries in the field, and eventually, through empirical evidence, help refine the tool towards a simplified version that can be widely used in practice. (link to template)

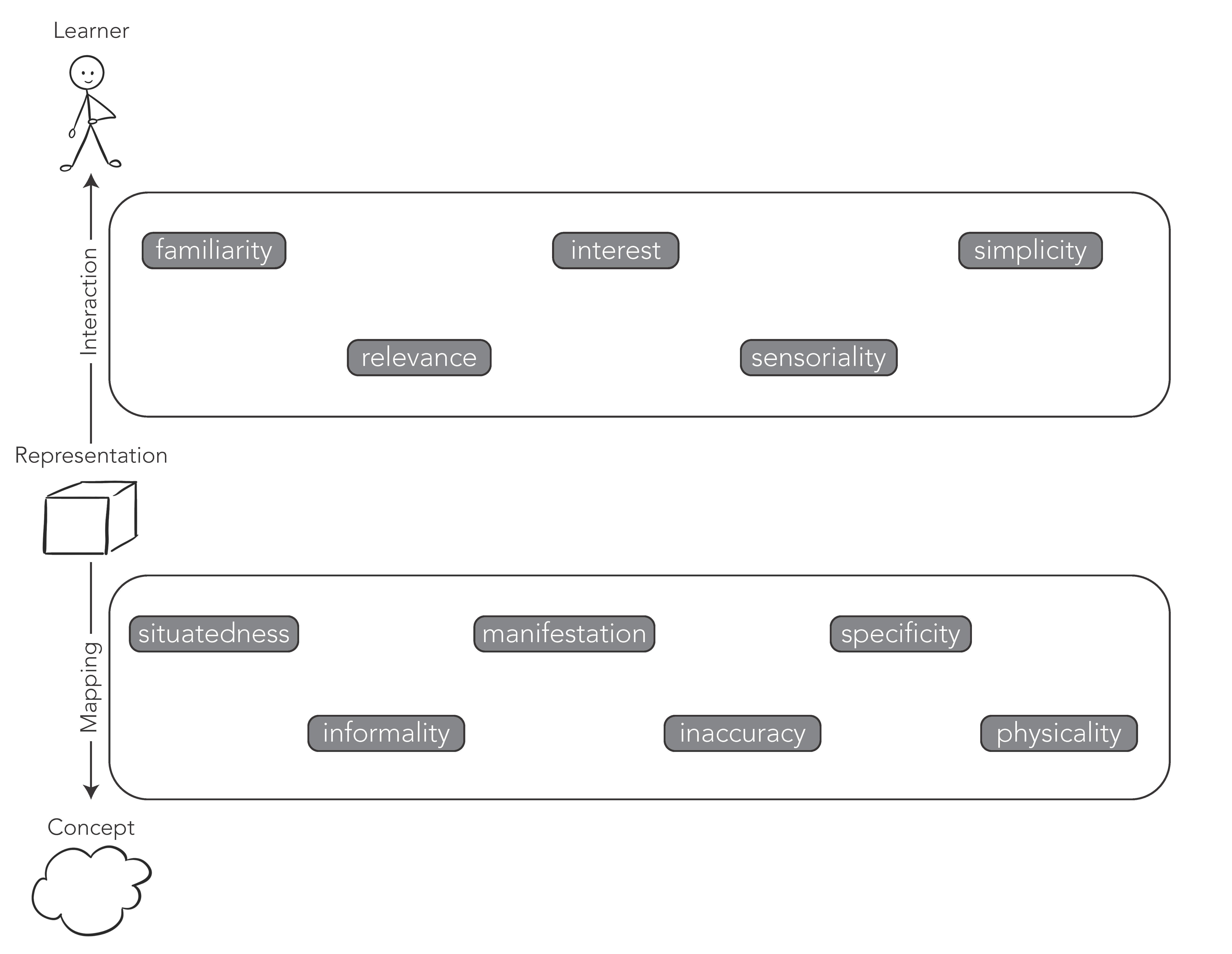
Second, we encourage scholars to use the tool to better situate their studies and designs in this landscape. As illustrated in our paper, we believe that this opens the floor to nuanced comparisons of existing studies, and further conversations about both design and learning processes leveraging concreteness and abstraction. We believe that our comprehensive taxonomy as well as these explorations can further facilitate future meta-analyses and reviews of the field. (link to template)

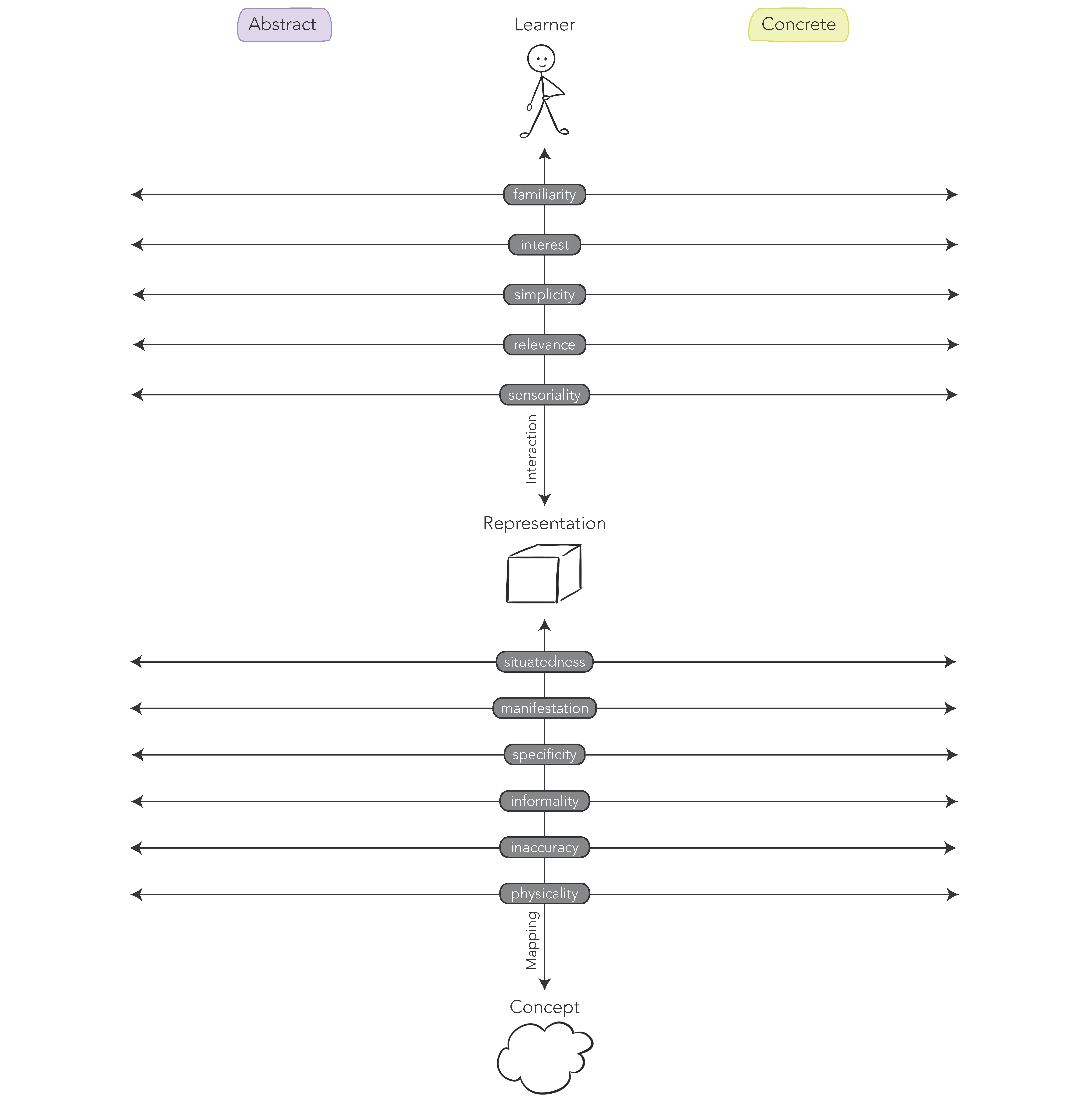
Third, we believe that this tool should evolve through practice and discussions in the community. Therefore, we would like to encourage researchers and practitioners alike to use the taxonomy to reflect on their own studies and design processes, and share their experiences and suggestions. While our approach is anchored in data, this tool is designed to evolve and improve through continued use. (link to template)

Team

• Julia Chatain - Concept, research, tool implementation, data annotation, analysis, paper writing
• Charlotte H. Müller - Concept, research, data annotation, analysis, paper writing
• Keny Chatain - Concept, research, data annotation, analysis, paper writing
• Leon Calabrese - Data collection, data annotation
• Manu Kapur - Supervision

Publications

Chatain, Julia, Charlotte H. Müller, Keny Chatain, Leon Calabrese, Manu Kapur. "Concreteness and Abstraction in Mathematics Education: A Taxonomy of the Semantic Landscape". Educational Psychology Review. (2025). (link) (pdf)

Chatain, Julia, Charlotte H. Müller, Keny Chatain, Leon Calabrese, Manu Kapur. "Towards a taxonomy of concreteness and abstraction in mathematics education". In the EARLI Conference. (2025).